Operasi Simetri Kristal

Simetri Kristal

Kristal, dan karena itu mineral, memiliki pengaturan internal yang teratur dari atom. Pengaturan ini memerintahkan menunjukkan simetri, yaitu atom-atom disusun secara simetris pada jaringan tiga dimensi disebut sebagai kisi. Ketika bentuk kristal dalam lingkungan di mana tidak ada hambatan untuk pertumbuhan, kristal menghadapi bentuk sebagai batas planar halus yang membentuk permukaan kristal. Wajah-wajah kristal mencerminkan pengaturan internal memerintahkan atom dan dengan demikian mencerminkan simetri kisi kristal. Untuk melihat ini, mari kita pertama bayangkan kristal kecil 2 dimensi yang terdiri dari atom dalam pengaturan internal teratur seperti yang ditunjukkan di bawah ini. Meskipun semua atom dalam kisi ini adalah sama, saya memiliki satu berwarna abu-abu dari mereka sehingga kita dapat melacak posisinya.

Jika kita memutar kristal sederhana dengan 90 o pemberitahuan bahwa kisi dan kristal tampak persis sama dengan apa yang kita mulai dengan. Putar lagi 90 o dan lagi sama nya. Lain rotasi 90 o lagi menghasilkan kristal yang identik, dan lain rotasi 90 o kembali kristal dengan orientasi aslinya. Dengan demikian, dalam 1 putaran o 360, kristal telah berulang, atau terlihat identik 4 kali. Dengan demikian kita mengatakan bahwa obyek ini memiliki 4 kali lipat simetri rotasi.

Simetri Operasi dan Elemen Sebuah operasi Simetri merupakan sebuah operasi yang bisa dilakukan baik secara fisik maupun imajinatif yang mengakibatkan tidak ada perubahan dalam penampilan obyek. Sekali lagi ditekankan bahwa dalam kristal, simetri bersifat internal, yang itu merupakan pengaturan geometris teratur dari atom dan molekul pada kisi kristal. Tapi, karena simetri internal tercermin dalam bentuk eksternal kristal yang sempurna, kita akan berkonsentrasi pada simetri eksternal, karena ini adalah apa yang dapat kita amati. Ada 3 jenis operasi simetri: rotasi, refleksi, dan inversi. Kita akan melihat masing-masing pada gilirannya.

Rotational Simetri Seperti digambarkan di atas, jika sebuah objek dapat diputar terhadap suatu sumbu dan berulang setiap 90 o rotasi maka dikatakan memiliki sumbu 4 kali lipat simetri rotasi. Sumbu rotasi sepanjang yang dilakukan adalah elemen simetri disebut sebagai sumbu rotasi. Berikut jenis sumbu simetri rotasi yang mungkin dalam kristal.

1-Lipat Rotasi Axis - Sebuah objek yang memerlukan rotasi dari 360 o penuh untuk mengembalikannya ke tampilan aslinya tidak memiliki simetri rotasi. Karena berulang 1 setiap kali o 360 dikatakan memiliki sumbu 1-kali lipat simetri rotasi.

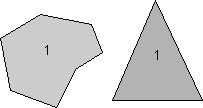2 kali lipat Axis Rotasi - Jika suatu benda muncul identik setelah rotasi 180 o, yang dua kali dalam rotasi o 360, maka dikatakan memiliki sumbu rotasi 2 kali lipat (360/180 = 2). Perhatikan bahwa dalam contoh ini sumbu kita mengacu kepada garis-garis imajiner yang membentang ke arah Anda tegak lurus ke halaman atau papan. Sebuah bentuk oval diisi merupakan titik di mana sumbu rotasi 2 kali lipat memotong halaman.

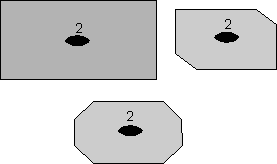Simbolisme ini akan digunakan untuk sumbu rotasi 2 kali lipat di seluruh kuliah dan dalam teks Anda.

3-Lipat Rotasi Axis - Objek yang berulang pada rotasi 120 o dikatakan memiliki sumbu 3-kali lipat simetri rotasi (360/120 = 3), dan mereka akan mengulangi 3 kali dalam rotasi o 360. Sebuah segitiga diisi digunakan untuk melambangkan lokasi 3 kali lipat sumbu rotasi.

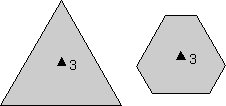4-Lipat Axis Rotasi - Jika suatu benda berulang setelah 90 o rotasi, itu akan mengulang 4 kali dalam rotasi o 360, seperti yang digambarkan sebelumnya. Sebuah persegi diisi digunakan untuk melambangkan lokasi 4 kali lipat sumbu simetri rotasi.

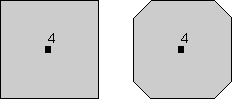6-Axis Rotasi Lipat - Jika rotasi 60 o terhadap suatu sumbu menyebabkan objek untuk mengulang sendiri, maka ia memiliki 6 kali lipat sumbu simetri rotasi (360/60 = 6). Sebuah heksagon diisi digunakan sebagai simbol untuk sumbu rotasi 6 kali lipat.

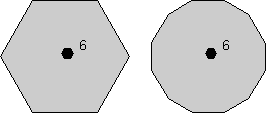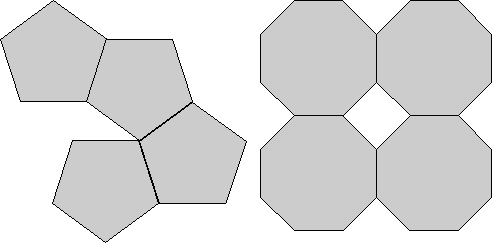
Meskipun obyek itu sendiri mungkin tampak memiliki 5 kali lipat, 7 kali lipat, 8 kali lipat, atau lebih tinggi kali lipat sumbu rotasi, ini tidak mungkin dalam kristal. Alasannya adalah bahwa bentuk eksternal kristal didasarkan pada susunan geometris dari atom. Perhatikan bahwa jika kita mencoba untuk menggabungkan objek dengan jelas simetri 5 kali lipat dan 8 kali lipat, bahwa kita tidak bisa menggabungkan mereka sedemikian rupa sehingga mereka benar-benar mengisi ruang, seperti yang digambarkan di bawah ini.

Cermin Simetri Sebuah operasi simetri cermin adalah operasi imajiner yang dapat dilakukan untuk mereproduksi obyek. Operasi ini dilakukan dengan membayangkan bahwa Anda memotong objek di setengah, kemudian menempatkan cermin di samping salah satu bagian dari objek di sepanjang memotong. Jika pantulan di cermin mereproduksi bagian lain dari objek, maka objek dikatakan memiliki simetri cermin. Pesawat cermin adalah elemen simetri disebut sebagai pesawat cermin, dan dilambangkan dengan huruf m. Sebagai contoh, tubuh manusia adalah obyek yang mendekati simetri cermin, dengan pesawat cermin memotong melalui pusat kepala, pusat hidung dan turun ke pangkal paha. Persegi panjang yang ditunjukkan di bawah memiliki dua pesawat simetri cermin.

The persegi panjang di sebelah kiri memiliki pesawat cermin yang berjalan secara vertikal pada halaman dan tegak lurus terhadap halaman. The persegi panjang di sebelah kanan memiliki pesawat cermin yang berjalan horizontal dan tegak lurus terhadap halaman. Bagian melesat dari persegi panjang di bawah ini menunjukkan bagian persegi panjang yang akan dilihat sebagai refleksi di cermin.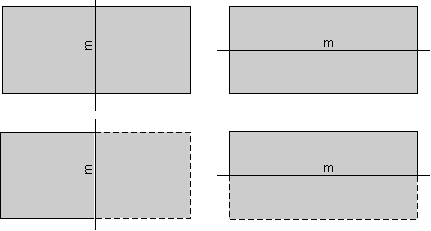

Persegi panjang yang ditunjukkan di atas memiliki dua pesawat simetri cermin. Tiga benda dimensi dan lebih kompleks bisa memiliki lebih. Misalnya, segi enam yang ditunjukkan di atas, tidak hanya memiliki sumbu rotasi 6 kali lipat, namun memiliki 6 pesawat cermin.

Perhatikan bahwa persegi panjang tidak memiliki simetri cermin sepanjang garis diagonal. Jika kita memotong persegi panjang sepanjang seperti diagonal seperti yang berlabel "m???", Seperti yang ditunjukkan dalam diagram atas, mencerminkan bagian bawah di cermin, maka kita akan melihat apa yang ditunjukkan oleh garis putus pada diagram yang lebih rendah. Karena ini tidak mereproduksi persegi panjang asli, baris "m???" tidak mewakili pesawat cermin.

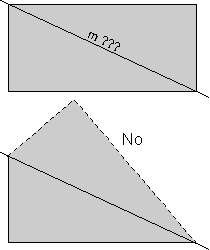Pusat Simetri Operasi lain yang dapat dilakukan adalah melalui inversi titik. Dalam operasi ini garis ditarik dari semua titik pada objek melalui titik di tengah objek, yang disebut pusat simetri (dilambangkan dengan huruf "i"). Garis masing-masing memiliki panjang yang berjarak sama dari titik awal. Ketika ujung garis yang terhubung, objek asli direproduksi terbalik dari penampilan aslinya. Dalam diagram ditampilkan di sini, hanya beberapa baris seperti beberapa yang diambil untuk wajah segitiga kecil. Diagram tangan kanan menunjukkan obyek tanpa garis imajiner yang direproduksi objek.

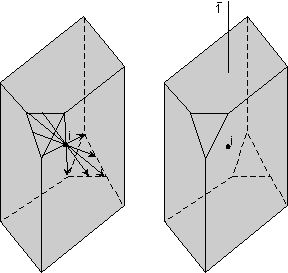Jika suatu benda hanya memiliki pusat simetri, kita mengatakan bahwa ia memiliki sumbu rotoinversion 1 kali lipat. Seperti sumbu memiliki simbol 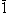, Seperti yang ditunjukkan dalam diagram tangan kanan di atas. Perhatikan bahwa kristal yang memiliki pusat simetri akan menunjukkan properti bahwa jika Anda letakkan di meja akan ada wajah di atas kristal yang akan sejajar dengan permukaan meja dan identik dengan wajah bertumpu pada table.

Rotoinversion Kombinasi rotasi dengan pusat simetri melakukan operasi simetri rotoinversion. Objek yang memiliki simetri rotoinversion memiliki unsur simetri yang disebut sumbu rotoinversion. Sebuah sumbu rotoinversion 1-lipat adalah sama sebagai pusat simetri, seperti yang dibahas di atas. Rotoinversion kemungkinan lainnya adalah sebagai berikut:

2 kali lipat Rotoinversion - Operasi 2 kali lipat rotoinversion melibatkan pertama memutar objek dengan 180 o kemudian pembalik melalui pusat inversi. Operasi ini setara dengan memiliki cermin tegak lurus dengan sumbu rotoinversion 2 kali lipat. Sebuah sumbu rotoinversion 2 kali lipat dilambangkan sebagai 2 dengan bar di atas, dan akan diucapkan sebagai "bar 2". Tapi, karena ini setara dengan sebuah pesawat cermin, m, 2 bar jarang digunakan.

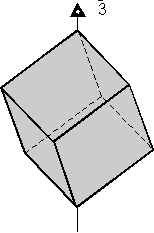
3-kali lipat Rotoinversion - Ini melibatkan memutar objek dengan 120 o (360/3 = 120), dan pembalik melalui pusat. Kubus adalah contoh yang baik dari sebuah benda yang memiliki 3 kali lipat sumbu rotoinversion. Sebuah sumbu rotoinversion 3 kali lipat dilambangkan sebagai 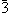(Diucapkan "bar 3"). Perhatikan bahwa sebenarnya ada empat 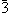sumbu dalam kubus, satu berjalan melalui setiap sudut kubus. Jika seseorang memegang salah satu 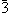sumbu vertikal, maka diketahui bahwa ada 3 wajah di atas, dan 3 wajah identik terbalik di bagian bawah yang offset dari wajah teratas dengan 120 o.

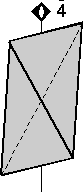
4 kali lipat Rotoinversion - Ini melibatkan rotasi objek dengan 90 o kemudian pembalik melalui pusat. Sebuah sumbu rotoinversion empat kali lipat dilambangkan sebagai 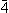. Perhatikan bahwa obyek yang memiliki 4 - sumbu rotoinversion kali lipat akan memiliki dua wajah di atas dan dua wajah identik terbalik di bagian bawah, jika 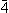sumbu dipegang dalam posisi vertikal.

6 kali lipat Rotoinversion - Sebuah sumbu rotoinversion 6 kali lipat ( 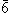) Melibatkan memutar objek dengan 60 o dan pembalik melalui pusat. Perhatikan bahwa operasi ini identik dengan memiliki kombinasi sumbu rotasi 3-kali lipat tegak lurus terhadap pesawat cermin.

Kombinasi Operasi Simetri Seperti harus jelas sekarang, dalam tiga dimensi benda, seperti kristal, elemen simetri dapat hadir dalam kombinasi yang berbeda. Bahkan, dalam kristal ada 32 kemungkinan kombinasi dari unsur-unsur simetri. Ini 32 kombinasi mendefinisikan Kelas Kristal 32. Setiap kristal harus dimasukkan ke salah satu dari kelas-kelas kristal 32. Pada kuliah mendatang kita akan mulai untuk pergi ke masing-masing kelas kristal secara rinci, tapi cara terbaik untuk dapat mengidentifikasi masing-masing kelas kristal tidak dengan mendengarkan saya kuliah, belum tentu dengan membaca tentang masing-masing kelas, namun sebenarnya melihat model kristal sempurna di laboratorium. Pada kenyataannya, itu adalah pendapat saya bahwa itu adalah mustahil untuk mengidentifikasi elemen simetri dan kelas kristal tanpa menghabiskan banyak waktu memeriksa dan mempelajari 3-dimensi model di laboratorium. Di sini, saya hanya akan memberikan satu contoh bagaimana elemen simetri berbagai digabungkan dalam kristal agak diselesaikan. Satu hal yang saya ingin menekankan dalam diskusi ini adalah bahwa jika 2 jenis elemen simetri yang hadir dalam kristal yang sama, maka mereka akan beroperasi pada satu sama lain untuk menghasilkan unsur-unsur lain simetri simetris. Ini harus menjadi jelas saat kita pergi ke contoh di bawah ini.

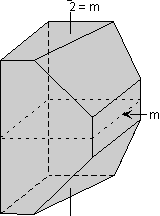
Dalam contoh ini kita akan mulai dengan kristal yang ditampilkan di sini. Perhatikan bahwa kristal ini memiliki berbentuk persegi panjang dengan sisi atas berbentuk persegi dan bawah. Bagian atas berbentuk persegi menunjukkan bahwa harus ada 4 kali lipat sumbu rotasi tegak lurus ke wajah berbentuk persegi. Hal ini ditunjukkan dalam diagram.

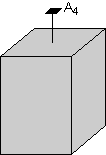Juga mencatat bahwa wajah berbentuk persegi panjang di sisi kiri dari kristal harus memiliki sumbu rotasi 2 kali lipat yang memotong itu. Perhatikan bahwa sumbu dua kali lipat berjalan melalui kristal dan keluar di sisi kiri (tidak terlihat dalam pandangan ini), sehingga baik kiri dan kanan - sisi tangan kristal tegak lurus terhadap sumbu rotasi 2 kali lipat.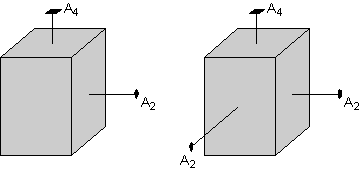

Karena wajah atas kristal memiliki sumbu rotasi 4 kali lipat, operasi ini rotasi 4 kali lipat harus mereproduksi wajah dengan tegak lurus 2 kali lipat sumbu rotasi pada 90 o. Dengan demikian, wajah depan dan belakang kristal juga akan memiliki tegak lurus 2 kali lipat sumbu rotasi, karena ini diperlukan oleh sumbu 4 kali lipat.

Bagian atas berbentuk persegi dari kristal juga menunjukkan bahwa harus ada sumbu 2 kali lipat yang memotong diagonal melalui kristal. Sumbu ini 2 kali lipat yang ditampilkan di sini dalam diagram kiri. Tapi, lagi-lagi operasi sumbu 4 kali lipat mensyaratkan bahwa diagonal lain juga memiliki 2 kali lipat sumbu, seperti yang ditunjukkan dalam diagram kanan.

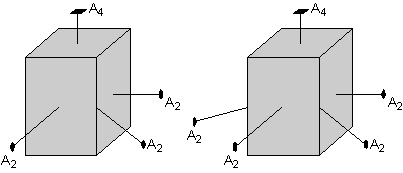Selain itu, bagian depan berbentuk persegi atas dan persegi panjang berbentuk kristal menunjukkan bahwa pesawat simetri hadir seperti yang ditunjukkan oleh diagram kiri-tangan di sini. Tapi, sekali lagi, operasi sumbu 4 kali lipat mensyaratkan bahwa pesawat cermin juga hadir yang memotong melalui sisi wajah, seperti yang ditunjukkan oleh diagram di sebelah kanan.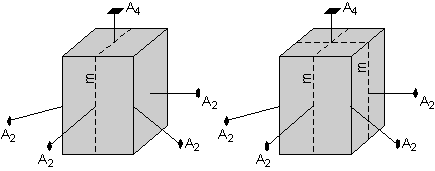

Bagian atas persegi lebih lanjut menunjukkan bahwa harus ada sebuah pesawat cermin memotong diagonal melalui kristal. Ini pesawat cermin akan dipantulkan oleh cermin pesawat lainnya memotong sisi kristal, atau akan direproduksi oleh sumbu rotasi 4 kali lipat, sehingga kristal akan memiliki pesawat lain cermin memotong melalui diagonal lainnya, seperti yang ditunjukkan oleh diagram di sebelah kanan.

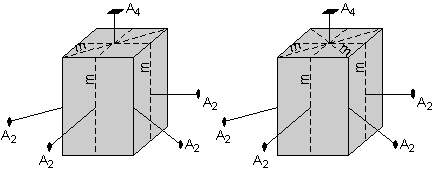Akhirnya, ada pesawat lain cermin yang memotong melalui pusat sejajar kristal ke wajah atas dan bawah.
Dengan demikian, kristal ini memiliki simetri elemen berikut: 1 - 4 kali lipat sumbu rotasi (A 4) 4 - sumbu rotasi 2 kali lipat (A 2), 2 memotong wajah & 2 memotong tepi. 5 mirror pesawat (m), 2 pemotongan seluruh wajah, 2 pemotongan melalui tepi, dan satu memotong secara horizontal melalui pusat. Perhatikan juga bahwa ada pusat simetri (i). Isi simetri kristal ini demikian: i, 1A 4, 4A 2, 5m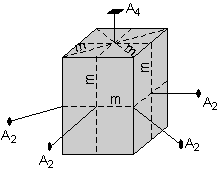

Jika Anda melihat Tabel 4.3 halaman 84 dari Hefferan & O'Brien, Anda akan melihat bahwa ini milik 4/m2/m2/m kelas kristal. Kelas ini adalah kelas dipyramidal ditetragonal.